Riemann Zeta -Funktion, Funktion in der Zahlentheorie zur Untersuchung der Eigenschaften von Primzahlen nützlich. Geschrieben als ζ (x), wurde es ursprünglich als die unendliche Serie ζ (x) = 1 + 2 definiert-x + 3-x + 4-x + ⋯. Wenn x = 1, wird diese Serie als Harmonic -Serie bezeichnet, die ohne gebundene zunimmt - ich.e., Seine Summe ist unendlich.
- Wofür ist die Riemann Zeta -Funktion, für die verwendet wird??
- Wie berechnen Sie die Funktion von Riemann Zeta??
- Wer löste die Riemann Zeta -Funktion?
- Wurde die Riemann Zeta -Funktion gelöst??
Wofür ist die Riemann Zeta -Funktion, für die verwendet wird??
Die Riemann Zeta-Funktion codiert Informationen über die Primzahlen-die Atome von arithmetischen und kritischen für die moderne Kryptographie, auf der der E-Commerce aufgebaut ist. Ein Beweis zu finden war der heilige Gral der Zahlentheorie, seit Riemann seine Hypothese erstmals veröffentlicht hat.
Wie berechnen Sie die Funktion von Riemann Zeta??
\ zeta (s) = \ sum_ n = 1^\ infty \ dfrac 1 n^s. ζ (s) = n = 1∑∞ ns1. Es wird dann durch analytische Fortsetzung einer meromorphen Funktion im gesamten C \ Mathbb C C durch eine funktionale Gleichung definiert.
Wer löste die Riemann Zeta -Funktion?
Die Werte der Riemann -Zeta -Funktion bei selbst positiven Ganzzahlen wurden von Euler berechnet. Die erste von ihnen, ζ (2), liefert eine Lösung für das Baselproblem. 1979 bewies Roger Apéry die Irrationalität von ζ (3).
Wurde die Riemann Zeta -Funktion gelöst??
Die Riemann -Hypothese, eine Formel im Zusammenhang mit der Verteilung der Primzahlen, ist seit mehr als einem Jahrhundert ungelöst.
 Howtosignalprocessing
Howtosignalprocessing
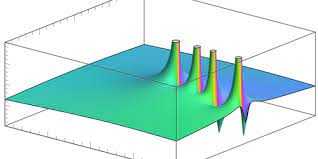

![Finden von x [0] aus dem Konvergenzbereich](https://howtosignalprocessing.com/storage/img/images_1/finding_x0_from_the_region_of_convergence.jpg)
![Beziehung / Verbindung zwischen maschinellem Lernen / Deep -Lernen und Computer Vision [geschlossen]](https://howtosignalprocessing.com/storage/img/images_1/relationship_connection_between_machine_learning_deep_learning_and_computer_vision_closed.jpg)